Maple计算器高级版 Maple计算器高级版是一款便捷的在线数学计算工具，它为每位用户提供了最简易的数据方程输入体验，旨在让用户能够轻松地进行在线数学公式的操作。该软件具备全网最佳的一键式方程分析功能，用户可以在此输入数据方程或公式，并得到智能化的解析结果，特别适合于正在学习数学的朋友，使学习过程变得更加简单高效。

Maple计算器高级版是一款便捷的在线数学计算工具，它为每位用户提供了最简易的数据方程输入体验，旨在让用户能够轻松地进行在线数学公式的操作。该软件具备全网最佳的一键式方程分析功能，用户可以在此输入数据方程或公式，并得到智能化的解析结果，特别适合于正在学习数学的朋友，使学习过程变得更加简单高效。

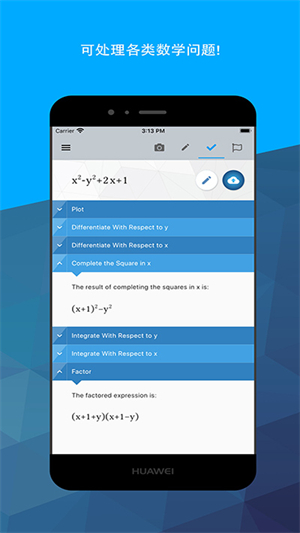
Maple计算器高级版应用程序提供了全新的图形化数据分析和解答功能，用户可以在这里一站式创建数学图表。它拥有全面的在线解析和详尽的公式解答，使每位用户都能在软件中轻松完成数据解析。

软件特色

1、 基本运算：算数、分数、小数、整数、因数、平方根、幂运算。

2、代数：线性方程组求解和绘图、方程组求解与绘图、处理多项式、二次方程与二次函数、对数函数与指数函数、三角函数、三角恒等式。

3、预科微积分：图形、分段函数、绝对值、不等式、隐函数。

软件亮点

1只需轻轻一点即可输入算式：通过相机一键点击，即可利用先进的人工智能技术录入手写或印刷的数学题目。此外，您还可以使用与老师相同的数学符号，在计算器中键入数学表达式——输入问题变得非常简单，因为这种方式看起来很直观！

2、执行多种数学计算：无论以何种方式输入数学问题，您都可以计算导数和积分、求解多项式方程、进行矩阵逆运算、解方程组以及常微分方程等。这款应用依托于世界顶尖的Maple数学引擎，能够处理大量的数学运算！

3、获得详细解题步骤：除了答案之外，还可以得到各种数学题的完整解题步骤，包括解方程组、求极限/导数/积分、完成矩阵运算等等！

4、图形问题求解：即刻查看表达式的二维和三维图形，观看改写表达式时图形会如何变化。您可以放大、平移甚至旋转三维图，以更仔细查看求解区域。

5、您离线时也能求解：应用的某些功能需要连接互联网，但您可随时使用图形计算器！

6、将计算结果直接上传到Maple Learn：使用相机将手写步骤自动发送到Maple Learn，您可以在其中发现错误并与他人分享您的工作。

7、避免在使用Maple桌面版时出现转写错误：为了防止在将数学表达式输入到Maple时发生错误，可以通过应用拍照并将图片上传至Maple，从而进一步研究和可视化。

8、支持国际语言：提供英语、西班牙语、法语、德语、俄语、丹麦语、瑞典语、日语和简体中文。

Maple计算器高级版怎么用

1、首先打开maple计算器手机版。

2、你可以随意输入公式、方程式等，可以清晰的查看到结果。

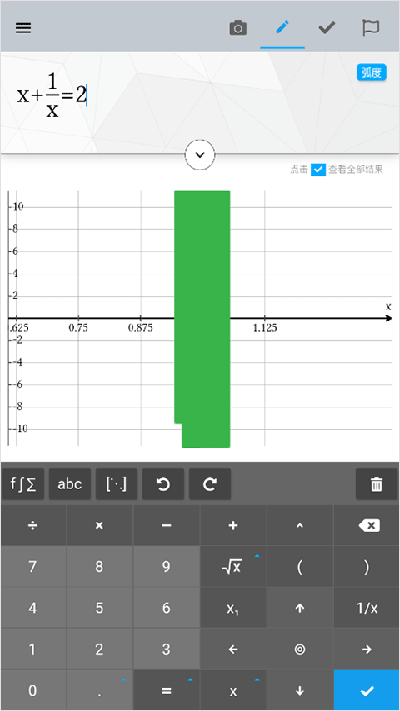
3、还可以输入复杂的方程式，也能自动显示计算的结果。

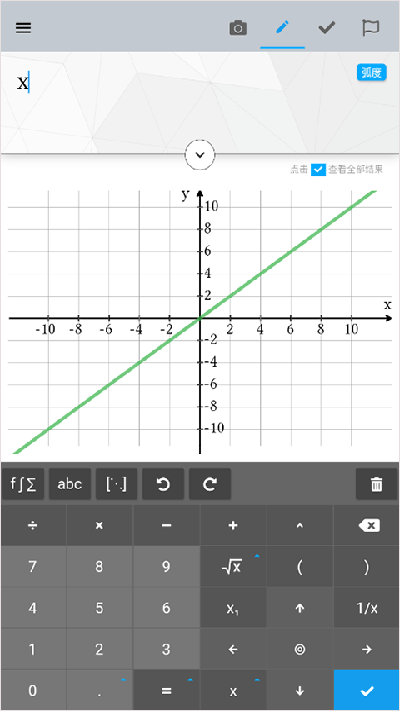
4、点击右上方按钮，还可以查看到方程两边的图。

5、求解x、化简、求微分等功能，非常好用。

Maple计算器高级版适用的领域

1、金融建模：金融函数包提供了丰富的工具，用于进行高级金融建模，涵盖个人财务管理，并适用于风险评估、证券投资管理、定量分析以及模型验证等领域。Maple 了大量函数命令，能够有效地支持模型的创建与计算。

2、物理领域：Maple 提供了丰富的函数和特殊函数工具，能够处理物理领域的多种计算问题，涵盖经典力学、量子力学、张量运算、常微分方程和偏微分方程的解析解求解、抽象向量代数、特殊函数以及电动力学等方面。

3、信号处理：Maple中提供了信号处理工具，可以用来分析和处理频域和时域的数据，这些工具被广泛应用于通信、滤波器设计、振动与噪声抑制以及数字信号处理等领域。

4、控制与设计：Maple中的函数库提供了丰富的数值和符号算法，适用于数据处理和可视化。此外，Maple工具包还包含多种工具，用于实现控制对象的建模以及高级控制系统的开发。

Maple计算器高级版怎么打平方

1、首先输入数字，然后点击图中的平方号

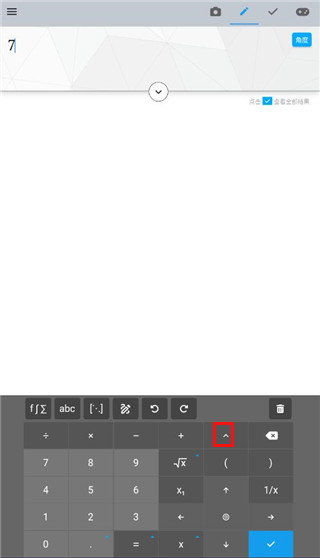
2、这样这个数的平方就即算出来了

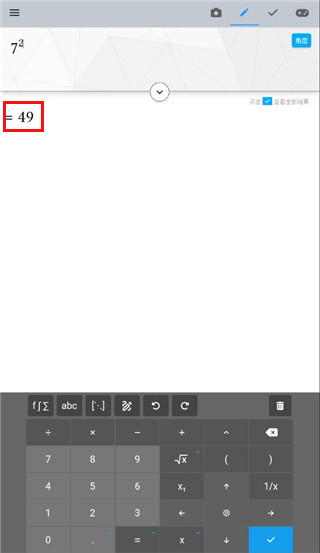
3、点击左上角的科学符号，还可以展开更多的数学符号

4、点击英文字母可以调出26个字母

5、当打出x的平方时，还可以绘制出x二次方的函数图

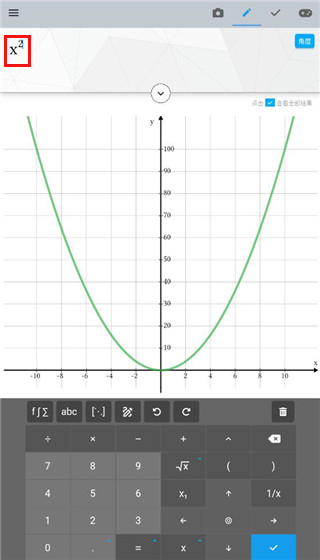
Maple计算器高级版解方程组

1）打开Maple，定义需要求解的方程组，如果输入的是矩阵形式，先将矩阵化成方程，输入方程组的系数矩阵A，点击回车，如下：

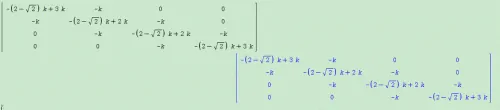
2）将方程写成[A]*[X]=0的形式，点击回车得到非矩阵形式的线性方程组，如下：

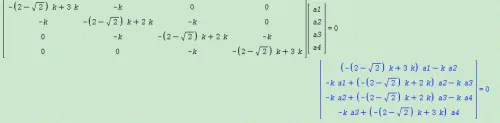
3）如上图，我们得到4个方程，现在将方程分开写成

（1）eqn1:=方程1=0；

（2）eqn2:=方程2=0；

（3）eqn3:=方程3=0；

（4）eqn4:=方程4=0；

具体，如下图表示：

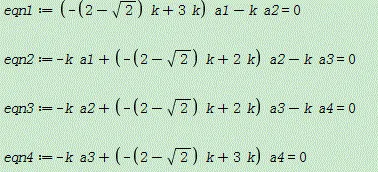
4）输入命令语句：solve（{eqn1，eqn2，eqn3，eqn4}，{a1,a2,a3,a4}）：

这里第一个“{}”中写需要求解的方程编号，第二个“{}”中写求解的变量，点击回车：